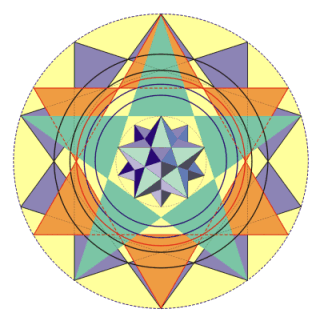
Auch auf dieser Seite wird zunächst ein kurzer Überblick über die Vorstellungen gegeben, die man sich in früheren Zeiten von der geometrischen Ordnung im Kosmos, d.h. hier in unserem Sonnensystem, gemacht hat. Der Begriff Geometrie bezieht sich dabei ausschließlich auf die Eigenschaften einfacher regulärer Figuren bzw. auf die Verhältnisse, welche in oder zwischen ihnen auftreten. Sodann folgen Beispiele für äußerst genaue Entsprechungen zwischen bestimmten regelmäßigen Figuren und der räumlichen Anordnung der Planeten.
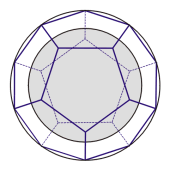
So wie die Idee von einer Sphärenharmonie seit Jahrtausenden in der Menschheit verankert ist, so wurde seit wohl ebenso langer Zeit ein Zusammenhang zwischen Geometrie und den himmlischen Verhältnissen erahnt. Platon brachte die fünf existierenden und nach ihm benannten regelmäßigen Körper mit den Elementen Feuer, Wasser, Erde, Luft und himmlisch-ätherische Substanz in Verbindung. Letztere ordnete er dem Dodekaeder zu, jener Figur, die von zwölf Fünfecken umgrenzt wird. Dem nebenstehenden Zwölfflächner ist dabei seine Inkugel eingeschrieben, welche die Mittelpunkte aller Seitenflächen berührt. Die durch den äußeren Kreis angedeutete Umkugel tangiert sämtliche 20 Ecken dieses platonischen Körpers.
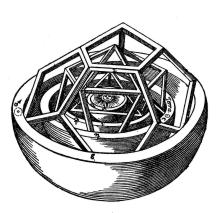
Auch in geometrischer Hinsicht war es erst Johannes Kepler, der die alten Vorstellungen knapp zwei Jahrtausende später weiterentwickelte. Ziemlich zu Beginn seiner Suche nach der Ordnung im Sonnensystem kreierte er ein Modell, wonach die Anordnung der sechs zu seiner Zeit bekannten Planeten durch die platonischen Körper geregelt wird. So entspricht beispielsweise das Verhältnis der Radien von Um- und Inkugel des Dodekaeders (allerdings nur sehr grob) demjenigen der Sonnenabstände von Mars und Erde. Die Inkugel wird nun zur Außenkugel eines Ikosaeders (ein anderer platonischer Körper, welcher von zwanzig gleichseitigen Dreiecken gebildet wird). Dessen Inkugel wiederum repräsentiert dann die Venusbahn usw.
Kepler war sich bewußt, daß die Übereinstimmung seines Modells mit den Werten der relativen Planetenabstände, so gut sie zu seiner Zeit vorlagen, nicht so genau war, wie er sich das wünschte. Von einer Verbesserung der Astronomie versprach er sich daher zunächst eine Austilgung der vorhandenen Abweichungen. Dies war eines der Hauptmotive, welche ihn zu seinen Forschungsarbeiten veranlaßten, deren Resultate das Weltbild der Menschheit für immer verändern sollten. Das erste seiner drei Planetengesetze besagt, daß die Bahnen der Planeten Ellipsen sind (und nicht vollkommene Kreise, wie man bis dahin dachte). Und um die geometrische Ordnung im Planetensystem zu verstehen, braucht man einen Begriff von den Parametern, welche eine Ellipse bestimmen.
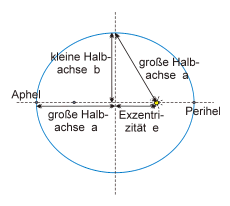
In einem der Brennpunkte planetarischer Ellipsenbahnen steht die Sonne. Die große Halbachse a stellt zugleich den mittleren Abstand des Planeten von unserem Lebensfeuer dar. Die Strukturiertheit des ganzen Systems, so wie sie sich in der Signatur der Spären kundtut, wird jedoch von den kleinen Halbachsen b vorgegeben. Am auffälligsten ist dabei zunächst, daß erster und vierter Planet, sowohl von innen als auch von außen gezählt, bezogen auf ihre kleinen Halbachsen im Verhältnis 4:1 stehen. Erster und sechster Planet, wiederum von innen und von außen gerechnet, weisen die Proportion 25:1 auf. Dadurch ergibt sich eine sehr klare übergeordnete Struktur, die von weiteren Verhältnissen kleiner ganzer Zahlen untergliedert wird. Diese Ordnung ist in der folgenden Abbildung durch entsprechende Kreise symbolisiert. Die Abweichungen von den realen Werten betragen jeweils nur wenige Promille, außer bei den Intervallen 8:3 bzw. 3:2, wo sie etwas über ein Prozent ausmachen. (Die genauen Werte finden sich in dem Buch Die Signatur der Sphären, S. 23 ff.)
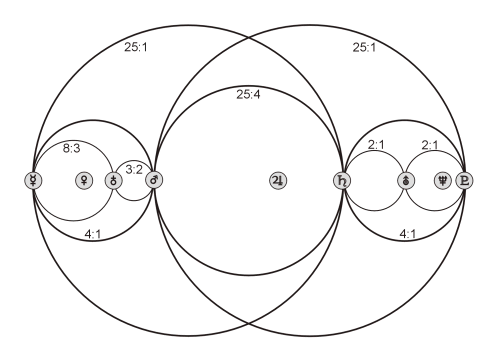
Es ist dies eine so bestechend klare und einfache Anordnung, daß man sich ein weiteres Mal wundern muß, warum diese bisher noch nicht entdeckt worden ist (nach unseren Kenntnissen jedenfalls). Es ist wie eine Spiegelung um Jupiter, das größte Mitglied der planetarischen Gemeinschaft. Er, die Venus und Neptun sind in die hier gezeigte Ordnung noch nicht integriert, was an anderer Stelle in der Signatur der Sphären jedoch erfolgt. Für die Venus sei exemplarisch die geometrische Konstruktion gezeigt, welche ihre kleine Halbachse mit derjenigen der Erde verbindet:
So sind schließlich überall die Verhältnisse einander gerade entgegengesetzt. In dieser Weise hat die Wunderwerke seiner Weisheit geschmückt er, der vor aller Zeit und in alle Ewigkeit ist. Nirgends ist etwas zuviel, nirgends etwas zu wenig da; nirgends ist ein Angriffspunkt für die Kritik. Wie lieblich sind seine Werke usw.! Alles ist gedoppelt; eines steht dem anderen gegenüber. Zu keinem fehlt das Gegenbild. Einem jeden hat er seine Vorzüge (Schmuck und Zier) sicher zugeteilt (durch beste Gründe festgesetzt), und wer bekommt je genug in der Betrachtung ihrer Herrlichkeit!
Johannes Kepler, Harmonice Mundi (Welt-Harmonik)
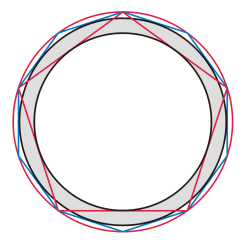
Einem Kreis wird ein Fünfeck umschrieben und dessen Umkreis ein Zehneck eingeschrieben. Der dann folgende Inkreis und der Grundkreis weisen ein Flächenverhältnis (1,38196:1) auf, welches der Proportion der kleinen Halbachsen von Erde und Venus fast hunderprozentig entspricht (Abweichung 0, 026 %). Daß dies mehr als ein bloßer Zufall sein dürfte, zeigt sich zum einen daran, daß das Intervall der Venus zu ihrem inneren Nachbarn, dem Merkur, genau das Quadrat dieser Proportion ausmacht (ebenfalls bei den kleinen Halbachsen). Geometrisch ließe sich dieser Wert durch die doppelte Ausführung der nebenstehenden Konstruktion erzielen. Zudem ergibt sich das gezeigte Verhältnis ebenso, wenn man den sonnennächsten Punkt der Marsbahn (Perihel) und die kleine Halbachse der Erde in Beziehung setzt. Stets betragen die Differenzen zu den realen planetarischen Werten weniger als 0,03 %. Aus all dem folgt, daß sich im Prinzip sämtliche Verhältnisse im inneren Planetensystem durch die Kombination von Fünfeck und Zehneck mit außerordentlicher Genauigkeit wiedergeben lassen. (Um auch die kleine Halbachse des Mars zu erfassen, tritt noch eine ebenso einfache Konstruktion mit dem Sechseck an Stelle des Fünfecks hinzu).
Daß diese Konstruktionsprinzipen auch die Verhältnisse im äußeren Planetensystem bestimmen und wie sie sich zu einem Gesamtbild zusammenfügen, wird im Kapitel 13 der Signatur der Sphären aufgezeigt. Es werden dort auch Hinweise gegeben, warum bei der räumlichen Anordnung der Planeten den kleinen Halbachsen die entscheidende Bedeutung zukommt und aus welchem Grund sich in deren Relationen – schließlich sind es Strecken – Flächenverhältnisse wiederfinden.