Johannes Kepler hat nicht nur die 3 Planetengesetze aufgefunden und eine Fülle von Hinweisen auf einen geheimnisvollen, harmonischen Aufbau unseres Sonnensystems gegeben, sondern auch zwei neue Sterne entdeckt. Es handelt sich dabei jedoch nicht um vormals unbekannte Körper am Himmel der Astronomie, sondern an demjenigen der Geometrie. Geht man z.B. von dem Dodekaeder aus, kommt man auf eine sehr einfache Weise zu der folgenden Figur:
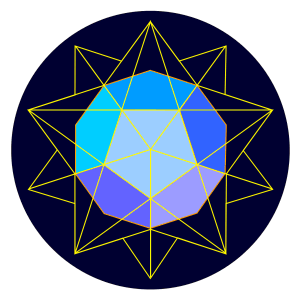
Man braucht nichts weiter zu tun, als die Kanten des Zwölfflächners bis zu ihren Schnittpunkten zu verlängern. Entsprechend erhält man aus dem Ikosaeder ebenso eine Sternfigur. Die Bedeutung Keplers für die geistige Entwicklung der Menschheit wird durch diese scheinbare geometrische Spielerei vielleicht am anschaulichsten demonstriert. Die platonischen Körper waren seit etwa zwei Jahrtausenden bekannt, doch vor ihm kam niemend auf diese einfache Idee. So wies Johannes Kepler nicht nur in der Astronomie (übrigens auch in der Optik), sondern auch in der Lehre von der Harmonie der Welt und der Geometrie neue Wege.
Der Dodekaederstern ist wahrscheinlich die harmonischste Figur, die sich überhaupt denken läßt. Er war Keplers Lieblingsstern, er gab ihm sogar den Kosenamen Igel. Daß der Igel auch für die Anordnung der Planetenbahnen eine Rolle spielt, ahnte Kepler, gegen Ende seiner Weltharmonik versuchte er, ihn in das Gefüge seiner Vorstellungen von der Harmonie der Sphären einzubauen. Es sollten jedoch noch weitere vier Jahrhunderte vergehen, bis sich herausstellte, daß die Strukturiertheit des inneren Planetensystems in diesem Keplerstern in der Tat seinen vollendeten Ausdruck findet.
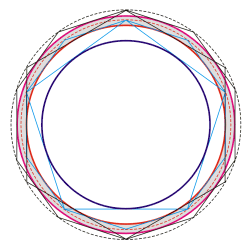 Auf der vorherigen Seite hatten wir erfahren, daß die Proportion der kleinen Halbachsen von Erde und Venus sich durch das Flächenverhältnis einer einfachen geometrischen Konstruktion sehr präzise annähern läßt. Nennen wir den entsprechenden Zahlenwert nun A (die mathematische Herleitung dieses und weiterer angesprochener Werte findet sich im Anhang der Signatur der Sphären). Das Intervall Venus-Merkur ergibt sich dann als A², dasjenige von Mars-Perihel zur kleinen Halbachse der Erde wiederum als A. Die Aphel-Distanz des Mars (sonnenfernster Punkt der Ellisenbahn) ist, wie bereits angedeutet, mit Hilfe des Sechseckes konstruierbar. So zeigt die nebenstehende Graphik – ausgehend von der Erde, blauer Kreis – die Konstruktion des Perihels (hellrot) über Fünfeck und Zehneck und die des Aphels (dunkelrot) über Sechseck und Zehneck. Der Zahlenwert beträgt 1,20601, nennen wir ihn B. Die kleine Halbachse des Mars läßt sich dann als geometrisches Mittel von Aphel und Perihel (= Wurzel (Aphel * Perihel)) finden, sie entspricht nahezu der roten, gestrichelten Hilfslinie.
Auf der vorherigen Seite hatten wir erfahren, daß die Proportion der kleinen Halbachsen von Erde und Venus sich durch das Flächenverhältnis einer einfachen geometrischen Konstruktion sehr präzise annähern läßt. Nennen wir den entsprechenden Zahlenwert nun A (die mathematische Herleitung dieses und weiterer angesprochener Werte findet sich im Anhang der Signatur der Sphären). Das Intervall Venus-Merkur ergibt sich dann als A², dasjenige von Mars-Perihel zur kleinen Halbachse der Erde wiederum als A. Die Aphel-Distanz des Mars (sonnenfernster Punkt der Ellisenbahn) ist, wie bereits angedeutet, mit Hilfe des Sechseckes konstruierbar. So zeigt die nebenstehende Graphik – ausgehend von der Erde, blauer Kreis – die Konstruktion des Perihels (hellrot) über Fünfeck und Zehneck und die des Aphels (dunkelrot) über Sechseck und Zehneck. Der Zahlenwert beträgt 1,20601, nennen wir ihn B. Die kleine Halbachse des Mars läßt sich dann als geometrisches Mittel von Aphel und Perihel (= Wurzel (Aphel * Perihel)) finden, sie entspricht nahezu der roten, gestrichelten Hilfslinie.
All diese Werte sind durch Kepler’s Igel zu dem Bild der vorherigen Seite verknüpft. Der innere blaue Kreis als Grundkreis entspricht dabei der Inkugel des dem Stern zugrunde liegenden Dodekaeders. Der nächste blaue Kreis stellt die Seitenansicht der Inkugel des Igels dar (das ist diejenige, die durch die Kanten des Dodekaeders hinausragt). Der mittlere rote Kreis ergibt sich aus der zweiten Seitenansicht des Dodekaedersterns, d.h. wenn man diesen um 18° dreht – bezogen auf die Ansicht des Sterns zu Beginn dieser Seite. Dann zeigt der Igel, daß in ihm auch ein Hexagramm verborgen liegt, wie das kleine Sternemblem (links oben auf allen Seiten) zeigt. Der rote Kreis ist der Umkreis des von dem Hexagramm gebildeten inneren Sechsecks; er weist zu dem Grundkreis den exakten Wert 5:3 auf (wiederum als Flächenverhältnisse der Kreise, d.h. der Seitenansichten der Kugeln). Die beiden schwarzen Kreise ergeben sich schließlich durch die Schnittpunkte des Zehnsterns, welchen der Igel in seiner anderen Seitenansicht präsentiert. Sämtliche Verhältnisse sind in der folgenden Tabelle zusammengestellt:
| Geometrisches Verhältnis | als Kombination von | Planetarisches Verhältnis der kleinen Halbachsen | Abweichung (%) | |
|---|---|---|---|---|
| Grundkreis | 1 | – | – | – |
| äußerer blauer Kreis | 1,381966 | A | Erde/Venus: 1,38233 Mars Pe/Erde: 1,38161 |
0,0264 0,0259 |
| roter Kreis | 1,666666 | A*B | Mars Ap/Erde: 1,66620 | 0,0279 |
| innerer schwarzer Kreis | 1,909830 | A² | Venus/Merkur: 1,90936 | 0,0249 |
| äußerer schwarzer Kreis | 2,639320 | A³ | Erde/Merkur: 2,63936 | 0,0015 |
Alle o.a. Verhältnisse im inneren Planetensystem sind also in Johannes Keplers Lieblingsstern in schlüssiger, d.h. kaum anders möglicher Weise angelegt. Den Grundkreis stellt eigentlich die Erde dar, denn alle ihre Proportionen zu den anderen inneren Planeten sind von diesem ausgehend vorgegeben. Somit kann man sagen, daß die Erde von dem himmlischen Äther des Dodekaeders bzw. seiner Sternerweiterung umgeben ist und ihre kleine Halbachse den Ausgangspunkt für sämtliche Proportionen bildet. Johannes Keplers Ahnungen, daß die platonischen Körper bzw. sein Igelstern mit den Verhältnissen im Sonnensystem in engster Weise zusammenhängen und daß die Erdbahn hierbei das Maß aller Dinge ist, haben sich, wenn auch in abgewandelter Form, auf eine fast unglaubliche Weise bestätigt.
