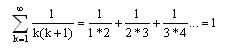
Diese Reihe ist lange bekannt (und auch die folgenden Umformungen). Ob sie einen offiziellen Namen trägt, weiß ich nicht, daher nenne ich sie die Eins-Reihe oder kurz ER.
Wie man sieht, sind in ihr alle Zahlen vorhanden, und sogar doppelt; bis auf die 1 selber, die Genüge hat, sich lediglich einmal zu zeigen. Rechts des Gleichheitszeichens erscheint sie dann aber doch ein zweites Mal als Summe der Reihe. Philosophisch gesprochen ist demnach in der Einheit (Eins) alles andere (alle anderen Zahlen) enthalten.
Daß ER tatsächlich gegen den Grenzwert 1 konvertiert, kann man sich leicht klar machen, indem man die Partialsummen bildet:
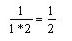
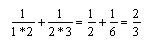
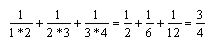
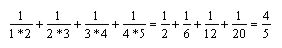
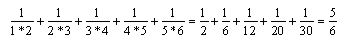
Musikalisch gesehen haben wir bis hier die einfachsten Schwingungsverhältnisse Oktave, Quinte, Quarte, Große und Kleine Terz. Spannt man eine Saite, unterteilt sie dann entsprechend und schlägt jeweils den kleineren Teilbereich an, erhält man die Obertöne der Saite – und dies läßt sich (theoretisch) bis ins Unendliche fortsetzen. In ER sind also auch alle Obertöne enthalten.
Nun formen wir die Reihe etwas um, und zwar mit Hilfe der einfachen Beziehung
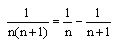
Der Beweis für diese Beziehung gelingt sehr einfach, in dem die rechte Seite ausmulipliziert wird. Damit ergibt sich, wenn man die einzelnen Glieder der Reihe ersetzt:
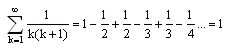
So gesehen, tauchen alle Zahlen in ER in positiver und negativer Form auf, wiederum bis auf die Eins, die nur positiv dasteht. In der Einheit (Eins) ist also nicht nur alles andere (alle anderen Zahlen) enthalten, sondern sogar in positiver und negativer Ausprägung. Die Einheit selbst kennt das Negative allerdings nicht. Sie – als das Allein-Gute gewissermaßen – ist jedoch nur vollständig, wenn alles andere mit seinen guten und schlechten Seiten mitzählt.
Hartmut Warm
